逻辑图


graph.png

graph (1).png

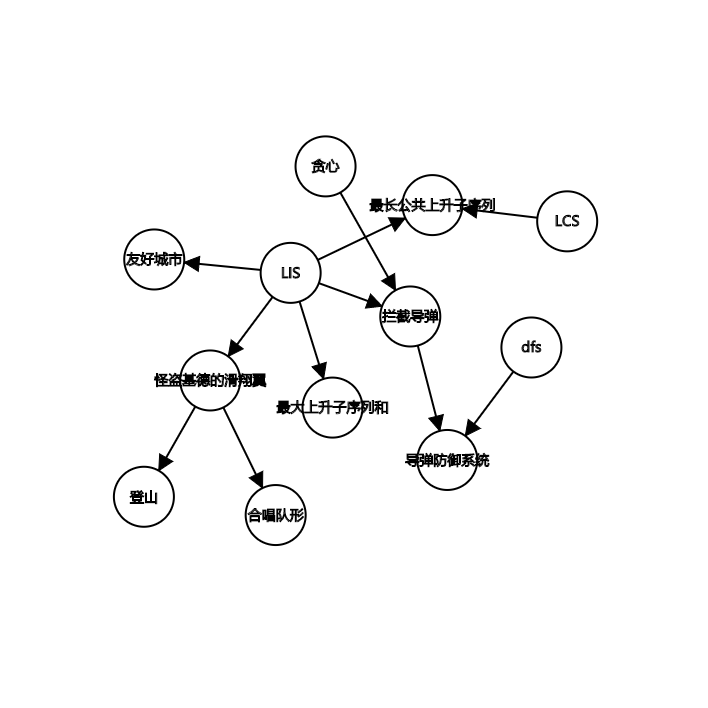
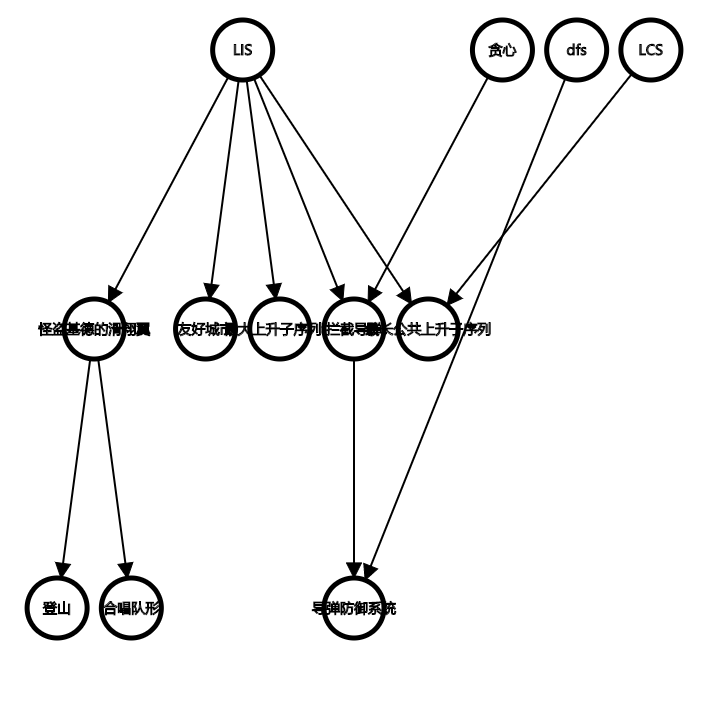
LIS 问题

题目链接

分析

状态表示 ( 即为 $f[i]$ 的表示)

集合 所有以 $a[i]$为结尾的严格单调上升子序列
属性 求最大值

状态计算 $f[i]$ 得来的过程

划分依据：“最后一个不同的点”

$f[i]$ 表示所有以 $a[i]$ 结尾的上升子序列

那么 $f[i]$ 是 所有 可能更新 $f[i]$ 的信息 中 取 最大值（属性）

那么 $f[i]$ 的所有可能性是 $f[1] - f[i - 1]$ 并且当 $a[i] < f[i]$ 时+1

Code 

#include <iostream>

using namespace std;

const int MAXN = 1e3;

int a[10001], f[1000];

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%d", &a[i]);
    }
    int res = 0;
    for (int i = 1; i <= n; i ++ )
    {
        f[i] = 1;
        for (int j = 1; j < i; j ++ )
        {
            if (a[j] < a[i])
            {
                f[i] = max(f[i], f[j] + 1);
            }
        }
        res = max(res, f[i]);
    }
    printf("%d", res);
    return 0;
}

怪盗基德的滑翔翼

题目链接

题目解析

有不同高度的楼房。怪盗基德在任意一个楼房开始。任意方向。要满足每次走到的高度 必须 比上次跳的高度低。

分析

当确定方向和七点后，最长的距离是以起点结尾的最长上升子序列。

所以我们可以以i为划分、1-i求最长上升子序列，n-i的最长上升子序列。

时间复杂度$O(n ^ {2})$

Code 

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

const int MAXN = 1e2 + 5;

int a[MAXN], f[MAXN];

int main()
{
    int t;
    scanf("%d", &t);
    while (t -- )
    {
        int n;
        scanf("%d", &n);
        for (int i = 1; i <= n; i ++ )
        {
            scanf("%d", &a[i]);
        }
        int res = 0;
        memset(f, 0, sizeof(f));
        for (int i = 1; i <= n; i ++ )
        {
            f[i] = 1;
            for (int j = 1; j < i; j ++ )
            {
                if (a[j] < a[i])
                {
                    f[i] = max(f[i], f[j] + 1);
                }
            }
            res = max(res, f[i]);
        }
        memset(f, 0, sizeof(f));
        for (int i = n; i >= 1; i -- )
        {
            f[i] = 1;
            for (int j = n; j > i; j -- )
            {
                if (a[j] < a[i])
                {
                    f[i] = max(f[i], f[j] + 1);
                }
            }
            res = max(res, f[i]);
        }
        printf("%d\n", res);
    }
    return 0;
}

登山

题目链接

题目解析

按照以下条件选择最多的浏览个数

  1. 按照编号递增的顺序浏览
  2. 相邻两个景点不能相同
  3. 一旦开始下降、不能上升。

目标：求最多能浏览的景点个数。

分析

  1. 按照编号递增的顺序浏览 => 必须是子序列
  2. 相邻两个景点不能相同
  3. 一旦开始下降、不能上升。 => 从某个点开始上升、从某个点再开始下降

即：
image.png

我们可以枚举顶峰的点。算一次正着的 $LIS$ 算一次倒着的 $LIS$ 然后相加求最大值即可。

Code 

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

const int MAXN = 1e3 + 5;

int a[MAXN], f[MAXN], fa[MAXN];

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%d", &a[i]);
    }
    int res = 0;
    for (int i = 1; i <= n; i ++ )
    {
        f[i] = 1;
        for (int j = 1; j < i; j ++ )
        {
            if (a[j] < a[i])
            {
                f[i] = max(f[i], f[j] + 1);
            }
        }
    }
    for (int i = n; i >= 1; i -- )
    {
        fa[i] = 1;
        for (int j = n; j > i; j -- )
        {
            if (a[j] < a[i])
            {
                fa[i] = max(fa[i], fa[j] + 1);
            }
        }
    }
    for (int i = 1; i <= n; i ++ )
    {
        res = max(res, fa[i] + f[i] - 1);
    }
    printf("%d\n", res);
    return 0;
}

合唱队形

题目链接

分析

要求求出挑出来多少个符合要求。那我们只用 把登山那道题的输出改成 $n - res$ 即可。

Code 

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

const int MAXN = 1e3 + 5;

int a[MAXN], f[MAXN], fa[MAXN];

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%d", &a[i]);
    }
    int res = 0;
    for (int i = 1; i <= n; i ++ )
    {
        f[i] = 1;
        for (int j = 1; j < i; j ++ )
        {
            if (a[j] < a[i])
            {
                f[i] = max(f[i], f[j] + 1);
            }
        }
    }
    for (int i = n; i >= 1; i -- )
    {
        fa[i] = 1;
        for (int j = n; j > i; j -- )
        {
            if (a[j] < a[i])
            {
                fa[i] = max(fa[i], fa[j] + 1);
            }
        }
    }
    for (int i = 1; i <= n; i ++ )
    {
        res = max(res, fa[i] + f[i] - 1);
    }
    printf("%d\n", n - res);
    return 0;
}

友好城市

毒瘤城市 （确信）

题目解析

条件：

  1. 每个城市上只能建立一个桥
  2. 所有桥与桥之间不能相交

目标：
最多可以建多少个桥

分析

每次选出的点是单调的点才不会出现相交。

否则 $100%$ 会出现相交.

Code 

#include <iostream>
#include <algorithm>

using namespace std;

const int MAXN = 5000;

int n;
pair<int, int> a[MAXN + 5];
int f[MAXN + 5];

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%d%d", &a[i].first, &a[i].second);
    }
    sort(a + 1, a + 1 + n);
    int res = 0;
    for (int i = 1; i <= n; i ++ )
    {
        f[i] = 1;
        for (int j = 1; j < i; j ++ )   
        {
            if (a[i].second > a[j].second)
            {
                f[i] = max(f[i], f[j] + 1);
            }
        }
        res = max(res, f[i]);
    }
    printf("%d", res);
    return 0;
}

最大上升子序列和

分析

$f[i]$ 状态表示

集合 所有以 $a[i]$为结尾的上升子序列和
属性 和 的 最大值

状态计算

$f[i]$

f[i] 分成( $i$ 类) 空, $a[1]$ , $a[2]$ , ... , $a[i - 1]$

第k类最大值 $f[k] + a[i]$

所以、与普通 $LIS$ 的关系从1变为 a[i]

Code 

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 1000;

int a[N + 1], n, f[N + 1];

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
    }
    int res = 0;
    for(int i = 1; i <= n; i++)
    {
        f[i] = a[i];
        for(int j = 1; j < i; j++)
        {
            if(a[j] < a[i])
            {
                f[i] = max(f[i], f[j] + a[i]);
            }
        }
        res = max(res, f[i]);
    }
    printf("%d", res);
    return 0;
}

拦截导弹

分析

对于某个点

选择：

  1. 接在某个现有的子序列之后
  2. 创建一个新的心痛

希望每次越大越好。

关于第二问：

贪心流程

对于每一个数：

出现的情况&解决

  1. 如果现在所有的子序列的结尾都小于当前数、那就创建一个新的子序列（新的导弹）
  2. 否则将当前数放到结尾大于等于它的最小的子序列后面。

$Dilworth$ 定理

代码 

#include <iostream>
#include <algorithm>

using namespace std;

int n,res;
int w[10001];
int f[10001],g[10001];

int main()
{
    while(cin >> w[n])
    {
        n++;
    }
    for(int i = 0; i < n; i++)
    {
        f[i] = 1;
        for(int j = 0; j < i; j++)
        {
            if(w[i] <= w[j])
            {
                f[i] = max(f[i], f[j] + 1);
            }
        }
        res = max(res, f[i]);
    }
    cout << res << endl;
    int c = 0;
    for(int i = 0; i <= n; i++)
    {
        int k = 0;
        while(k < c && g[k] < w[i])
        {
            k++;
        }
        g[k] = w[i];
        if(k >= c)
        {
            c++;
        }
     }
     cout << c;
     
    return 0;
}

导弹防御系统

题目解析

显然这是一个既可能上升又会下降的 $LIS$ 问题。

分析

显然、我们可以打个dfs暴力

每次要么安插到在上升、要么在下降

Code 

#include <iostream>
#include <cstdio>

using namespace std;


const int N = 50 + 5;

int res, as[N], up[N], down[N], m, n;

void dfs(int u, int a, int b)
{
    if (a + b >= res)
    {
        return ;
    }
    if (u == n)
    {
        res = min(res, a + b);
        return ;
    }
    int k = 0;
    while (k < a && up[k] >= as[u])
        k ++;
    int t = up[k];
    up[k] = as[u];
    if (k < a)
    {
        dfs(u + 1, a, b);
    }
    else
    {
        dfs(u + 1, a + 1, b);
    }
    up[k] = t;
    k = 0;
    while (k < b && down[k] <= as[u])
        k ++;
    t = down[k];
    down[k] = as[u];
    if (k < b)
    {
        dfs(u + 1, a, b);
    }
    else
    {
        dfs(u + 1, a, b + 1);
    }
    down[k] = t;
    
}

int main()
{
    while (cin >> n, n)
    {
        for (int i = 0; i < n; i ++ )
        {
            scanf("%d", &as[i]);
        }
        res = n;
        dfs(0, 0, 0);
        printf("%d\n", res);
    }
    return 0;
}

最长公共上升子序列

分析

需要上升、公共。

状态表示

$f[i][j]$ 来表示 所有由第一i个序列的前 $i$ 个字母、和第二个序列的前 $j$个字母构成的，且以 $b[j]$ 结尾的公共上升子序列

属性： 求最大值

状态计算

所有包含 $a[i]$ 的公共上升子序列 以及 所有不包含的 $a[i]$ 的公共上升子序列。

Code 

#include <iostream>
#include <cstdio>

using namespace std;


const int N = 50 + 5;

int res, as[N], up[N], down[N], m, n;

void dfs(int u, int a, int b)
{
    if (a + b >= res)
    {
        return ;
    }
    if (u == n)
    {
        res = min(res, a + b);
        return ;
    }
    int k = 0;
    while (k < a && up[k] >= as[u])
        k ++;
    int t = up[k];
    up[k] = as[u];
    if (k < a)
    {
        dfs(u + 1, a, b);
    }
    else
    {
        dfs(u + 1, a + 1, b);
    }
    up[k] = t;
    k = 0;
    while (k < b && down[k] <= as[u])
        k ++;
    t = down[k];
    down[k] = as[u];
    if (k < b)
    {
        dfs(u + 1, a, b);
    }
    else
    {
        dfs(u + 1, a, b + 1);
    }
    down[k] = t;
    
}

int main()
{
    while (cin >> n, n)
    {
        for (int i = 0; i < n; i ++ )
        {
            scanf("%d", &as[i]);
        }
        res = n;
        dfs(0, 0, 0);
        printf("%d\n", res);
    }
    return 0;
}

That`s all

最后修改：2020 年 08 月 16 日
© 禁止转载
End.