概括
状态压缩DP大概分为两大类
棋盘式(连通性)
集合式
小国王
题目
在 $n×n$ 的棋盘上放 $k$ 个国王,国王可攻击相邻的 $8$ 个格子,求使它们无法互相攻击的方案总数。
输入格式
共一行,包含两个整数 $n$ 和 $k$。
输出格式
共一行,表示方案总数,若不能够放置则输出 $0$。
数据范围
$1≤n≤10$
$0≤k≤n$
输入样例
3 2输出样例
16题目解析
他的攻击范围是一个井字形。
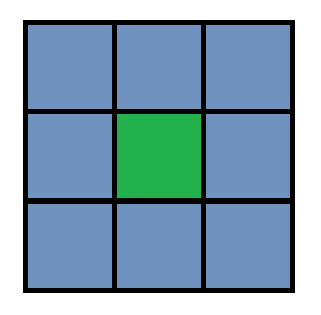
除了中间、其他位置均不可有将军。
那么我们来分析样例中的 $n = 3$ $k = 2$ 时的棋盘个数。
为了方便起见、我直接将他们放在一张图 、放在一张图占地面积可能小一点[heimu]明明是你懒 →_→[/heimu]
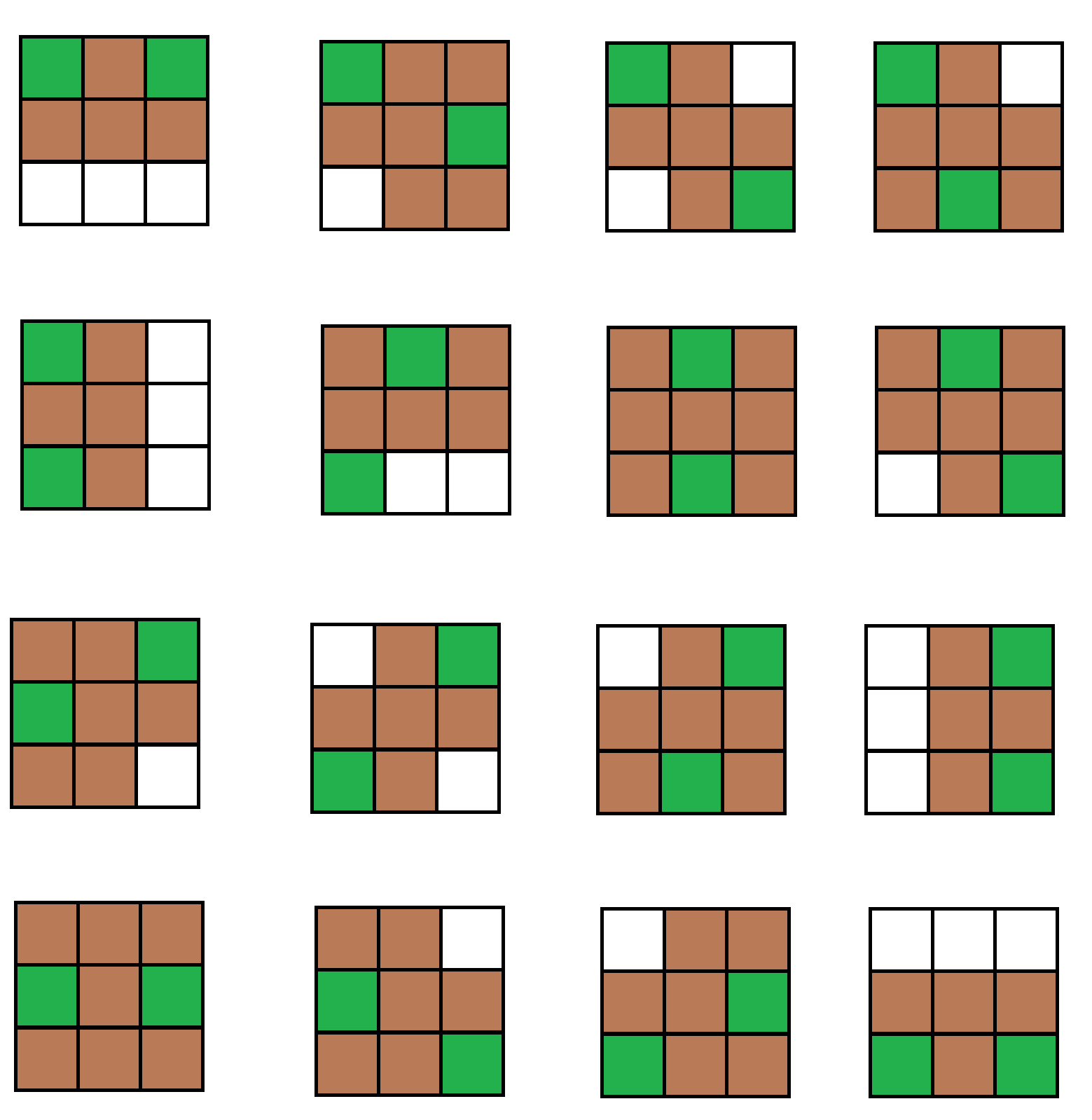
分析
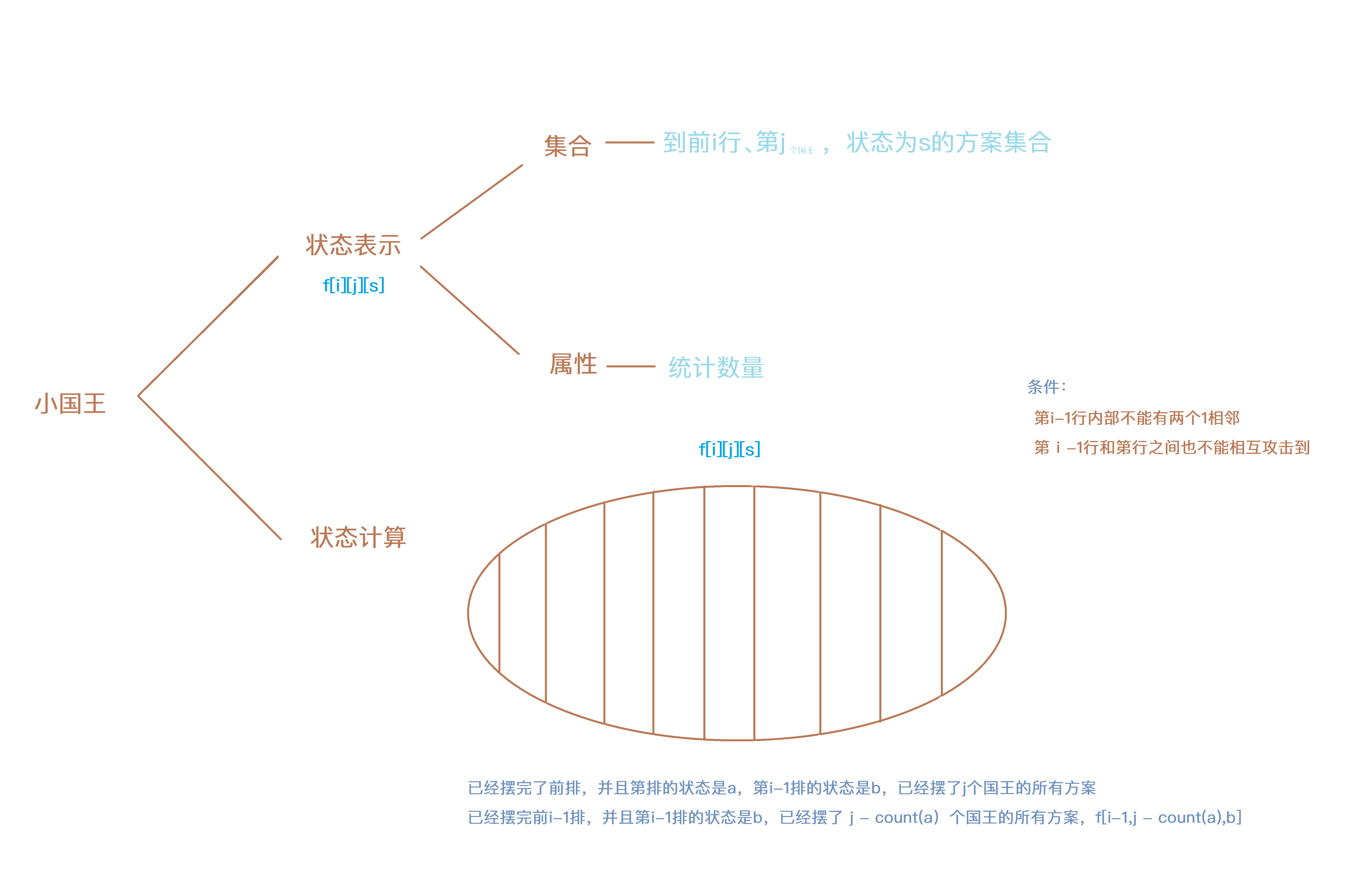
Code
#include <iostream>
#include <vector>
#include <queue>
#include <cstdio>
using namespace std;
const int N = 15, M = (1 << 10) + 15, K = 100 + 15;
typedef long long LL;
vector<int> status;
vector<int> h[M];
LL f[N][K][M];
int n, k, cnt[M];
bool check(int x)
{
for (int i = 0; i < n; i ++ )
{
if ((x >> i & 1) && (x >> i + 1 & 1))
{
return false;
}
}
return true;
}
int cnts(int s)
{
int res = 0;
for (int i = 0; i < n; i ++ )
{
res += s >> i & 1;
}
return res;
}
int main()
{
scanf("%d%d", &n, &k);
int lenn = 1 << n;
for (int i = 0; i < lenn; i ++ )
{
if (check(i))
{
status.push_back(i);
cnt[i] = cnts(i);
}
}
int len = status.size();
for (int i = 0; i < len; i ++ )
{
for (int j = 0; j < len; j ++ )
{
int a = status[i], b = status[j];
if ((a & b) == 0 && (check(a | b)))
{
h[i].push_back(j);
}
}
}
f[0][0][0] = 1;
for (int i = 1; i <= n + 1; i ++ )
{
for (int j = 0; j <= k; j ++ )
{
for (int a = 0; a < len; a ++ )
{
int len2 = h[a].size();
for (int b = 0; b < len2; b ++ )
{
int ne = h[a][b];
int c = cnt[status[a]];
if (j >= c)
{
f[i][j][a] += f[i - 1][j - c][ne];
}
}
}
}
}
printf("%lld", f[n + 1][k][0]);
return 0;
}玉米田
题目
题目描述
农夫约翰的土地由 $M*N$ 个小方格组成,现在他要在土地里种植玉米。
非常遗憾,部分土地是不育的,无法种植。
而且,相邻的土地不能同时种植玉米,也就是说种植玉米的所有方格之间都不会有公共边缘。
现在给定土地的大小,请你求出共有多少种种植方法。
土地上什么都不种也算一种方法。
输入格式
第1行包含两个整数 $M$ 和 $N$ 。
第 $2..M+1$ 行:每行包含N个整数 $0$ 或 $1$ ,用来描述整个土地的状况,1表示该块土地肥沃,$0$ 表示该块土地不育。
输出格式
输出总种植方法对 $100000000$ 取模后的值。
数据范围
$1≤M,N≤12$
输入样例:
2 3
1 1 1
0 1 0输出样例:
9[heimu]奶牛去哪了[/heimu]
题目解析
有些土地不能碰。而且、土地之间必须相隔一个。
分析
也就是说本题比上题多了个条件。有些田天生不能种地。
当然比上题轻松在于、这是个十字形。
所以理解好上道题即可
Code
#include <iostream>
#include <vector>
using namespace std;
const int N = 15, K = (1 << 12) + 5, mod = 1e8;
int f[N][K], m, n, g[N];
vector<int> status, head[N];
bool check(int x)
{
for (int i = 0; i < m; i ++ )
{
if ((x >> i & 1) && (x >> i + 1 & 1))
{
return false;
}
}
return true;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ )
{
for (int j = 0; j < m; j ++ )
{
int x;
scanf("%d", &x);
g[i] += !x << j;
}
}
int lena = 1 << m;
for (int i = 0; i < lena; i ++ )
{
if (check(i))
{
status.push_back(i);
}
}
int len = status.size();
for (int i = 0; i < len; i ++ )
{
for (int j = 0; j < len; j ++ )
{
int a = status[i];
int b = status[j];
if ((a & b) == 0)
{
head[i].push_back(j);
}
}
}
f[0][0] = 1;
for (int i = 1; i <= n + 1; i ++ )
{
for (int j = 0; j < len; j ++ )
{
int lens = head[j].size();
for (int k = 0; k < lens; k ++ )
{
int a = status[j], b = head[j][k];
if (g[i] & a)
{
continue;
}
f[i][j] = (f[i][j] + f[i - 1][b]) % mod;
}
}
}
printf("%d", f[n + 1][0] % mod);
}炮兵阵地
题目解析
往左右上下多延伸一格、跟上一题很相似 [heimu]显然你还是不会写。[/heimu]
要求的答案虽然发生了变化。但只需要我们改动一下即可
分析
对于普通的状态压缩DP.所有问题与求解。
- a、b、C不相等
解决方案: $((a \& b) | (a \& c) | (b \& c) )$ - 需要保证在平地。
解决方案:$(g[i-1] \& a | g[i] \& b ) == 0$
Code
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
const int N = 1e2 + 5, M = 12, K = (1 << 10) + 5;
int f[2][K][K], g[N], cnt[K];
vector<int> status, head[N];
int n, m;
bool check(int x)
{
for (int i = 0; i < m; i ++ )
{
if ((x >> i & 1) && (x >> i + 1 & 1 | x >> i + 2 & 1))
{
return false;
}
}
return true;
}
int cnts(int x)
{
int cntf = 0;
for (int i = 0; i < m; i ++ )
{
cntf += x >> i & 1;
}
return cntf;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ )
{
for (int j = 0; j < m; j ++ )
{
char x;
cin >> x;
g[i] += (x == 'H') * (1 << j);
}
}
int lena = 1 << m;
for (int i = 0; i < lena; i ++ )
{
if(check(i))
{
status.push_back(i);
cnt[i] = cnts(i);
}
}
int len = status.size();
for (int i = 1; i <= n + 2; i ++ )
{
for (int a = 0; a < len; a ++ )
{
for (int b = 0; b < len; b ++ )
{
for (int c = 0; c < len; c ++ )
{
int x = status[a], y = status[b], z = status[c];
if ((x & y) | (y & z) | (x & z))
{
continue;
}
if ((g[i - 1] & x) | (g[i] & y))
{
continue;
}
f[i & 1][a][b] = max(f[i & 1][a][b], f[(i - 1) & 1][c][a] + cnt[y]);
}
}
}
}
printf("%d", f[(n + 2) & 1][0][0]);
}最短Hamilton路径
There will be something here.
Code
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int w[21][21];
int f[1 << 21][22];
int main()
{
int n;
scanf("%d", &n);
memset(f, 0x3f, sizeof f);
for(int i = 0; i < n; i ++ )
{
for(int j = 0; j < n; j ++ )
{
scanf("%d", &w[i][j]);
}
}
f[1][0] = 0;
for(int i = 0; i < (1 << n); i ++ )
{
for(int j = 0; j < n; j ++ )
{
if((i >> j) & 1)
{
for(int k = 0; k < n; k ++ )
{
if((i ^ 1 << j) >> k & 1)
{
f[i][j] = min(f[i][j], f[i ^ 1 << j][k] + w[k][j]);
}
}
}
}
}
printf("%d", f[(1 << n) - 1][n - 1]);
return 0;
}