算是结束了
有向图中的联通分量
通常在有向图中我们会关心 极大联通分量 / 强联通分量 ( SCC ) 。我们考虑定义:
定义
联通分量定义为:选中 $(V, E)$ 中 任意两点可互达。
最大联通分量定义为:在选中 $(V, E)$ 中,符合联通分量。在添加其他任意点将不再符合定义。
我们可以看成一颗树。和一些其他边构成:
- 树边:看成树上的边
- 后向边:看成一个树上从前向后的指向
- 前向边:看成一个树上从后向前的指向
- 交叉边:看成指向非直接祖先的边
以上定义可能均有所不同叫法。但是实质相差不大。我们可以用一个图来表示。
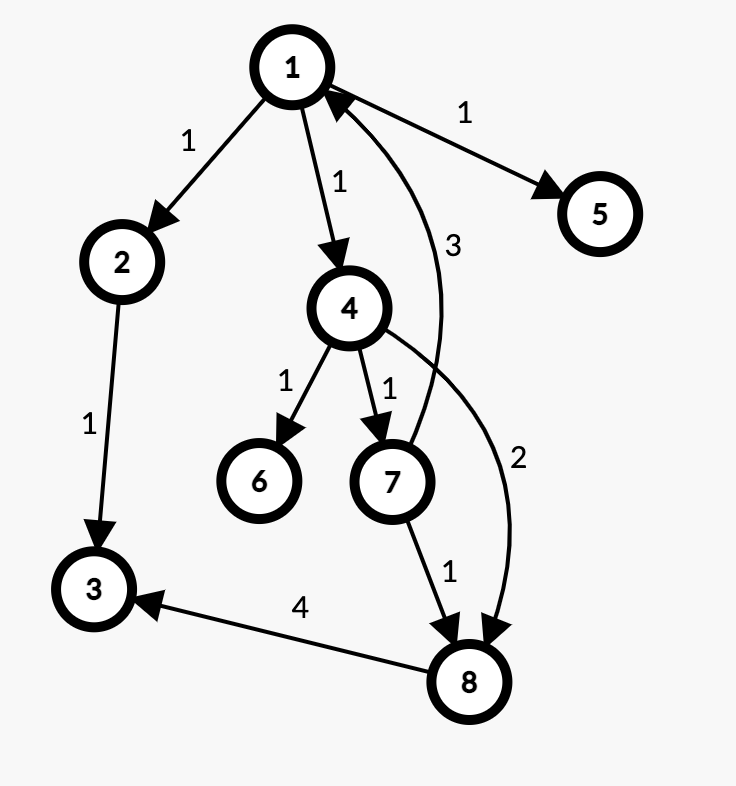
图片中的id对应上方的定义相匹配。
Tarjan 解决 SCC
tarjan是一种解决SCC问题的正确的且线性的方式。
我们通常找到SCC并进行 缩点 操作。即构成的SCC缩为一个点,并忽略其中内部的构造。最终使得图片变为一个 DAG。使其具有更优的性质。
我们考虑tarjan的解决方式。我们定义一个 $dfn_i$ 和 $low_i$ 分别表示 $dfs$ 序( $dfn_i$ ) 和 对于当前点能到达最低的 $dfn_i$ ( $low_i$ )
我们发现当 $dfn_i == low_i$ 是是一个 SCC 中的一个点。
那么我们可以写出一个模版:
dfn[u] = low[u] = ++ idx;
stk[++ top] = u, in_stk[u] = true;
for (int v : g[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (in_stk[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
scc_cnt ++;
seq.push_back(scc_cnt);
while (true) {
int v = stk[top --];
in_stk[v] = false;
scc[v] = scc_cnt;
scg[scc_cnt] += a[v];
if (v == u) {
break;
}
}
}然后可以进一步进行缩点。
SCC通常需要考虑缩点后的做法。我们发现 DAG 可以进行topo排序并完成相关题目。
P2812 校园网络
我们考虑缩点后我们只需要观察几个起点或者终点。
第一问的答案是所有出度为 $0$ 的点数量。
第二问的答案是所有出度为 $0$ 的点 或者 入读为 $0$ 的点最小值。
我们发现第一问的正确性显然。
我们来试着证明第二问。
第二问即要求我们要求出最少能将整个图覆盖的。
我们考虑因为建的边可以自定方向。所以可以将这个 出度为 $0$ 的点 或者 入读为 $0$ 的点 进行反转来处理。
我们发现只要任意两个相邻的终点(或起点)链接。最后第一个链接起点。
Code:
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
using namespace std;
const int N = 1e5 + 5;
int x;
vector<int> g[N];
int low[N], dfn[N], scc[N], in_stk[N], idx, scc_cnt, stk[N], top;
int rd[N], cd[N];
void tarjan(int u) {
dfn[u] = low[u] = ++ idx;
in_stk[u] = true;
stk[++ top] = u;
for (int v : g[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (in_stk[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (low[u] == dfn[u]) {
scc_cnt ++;
while (true) {
int v = stk[top --];
in_stk[v] = false;
scc[v] = scc_cnt;
if (v == u) {
break;
}
}
}
}
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i ++ ) {
while (cin >> x) {
if (x == 0) {
break;
}
g[i].push_back(x);
}
}
for (int i = 1; i <= n; i ++ ) {
if (!dfn[i]) {
tarjan(i);
}
}
for (int i = 1; i <= n; i ++ ) {
for (int j : g[i]) {
if (scc[i] != scc[j]) {
rd[scc[i]] ++;
cd[scc[j]] ++;
}
}
}
int r = 0, c = 0;
for (int i = 1; i <= scc_cnt; i ++ ) {
if (!rd[i]) {
r ++;
}
if (!cd[i]) {
c ++;
}
}
cout << r << '\n' << min(r, c) << endl;
return 0;
}P2272 最大半联通子图
较为麻烦的题意。简洁来说就是缩点之后选一条链。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <map>
using namespace std;
typedef long long ll;
const int N = 1e5 + 5, M = 2e5 + 5;
vector<int> g[N], gf[N];
map<int, int> dd;
int n, m;
ll MOD;
int dfn[N], low[N], idx, stk[N], top, in_stk[N], scc[N], ac[N], scc_cnt;
void tarjan(int x) {
dfn[x] = low[x] = ++ idx;
stk[++ top] = x, in_stk[x] = 1;
for (int ver : g[x]) {
if (!dfn[ver]) {
tarjan(ver);
low[x] = min(low[x], low[ver]);
} else if (in_stk[ver]) {
low[x] = min(low[x], dfn[ver]);
}
}
if (dfn[x] == low[x]) {
scc_cnt ++ ;
while (true) {
int v = stk[top -- ];
in_stk[v] = 0;
scc[v] = scc_cnt;
ac[scc_cnt] ++;
if (x == v) {
break;
}
}
}
}
ll f[N], ra[N];
int main() {
cin >> n >> m;
cin >> MOD;
for (int i = 1; i <= m; i ++ ) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
}
for (int i = 1; i <= n; i ++ ) {
if (!dfn[i]) {
tarjan(i);
}
}
for (int i = 1; i <= n; i ++ ) {
for (int ver : g[i]) {
if (scc[i] != scc[ver]) {
gf[scc[i]].push_back(scc[ver]);
}
}
}
for (int i = 1; i <= scc_cnt; i ++ ) {
ra[i] = 1;
}
for (int i = 1; i <= scc_cnt; i ++ ) {
f[i] = ac[i];
dd.clear();
for (int ver : gf[i]) {
if (f[i] < f[ver] + ac[i]) {
f[i] = f[ver] + ac[i];
dd[ver] = true;
ra[i] = ra[ver];
} else if (f[ver] + ac[i] == f[i]) {
ra[i] += (!dd[ver]) * ra[ver];
dd[ver] = true;
ra[i] %= MOD;
}
}
}
ll rt = 0, rea = 0;
for (int i = 1; i <= scc_cnt; i ++ ) {
if (f[i] > rt) {
rt = f[i];
rea = ra[i];
} else if (f[i] == rt) {
rea += ra[i];
rea %= MOD;
}
}
cout << rt << '\n';
cout << rea % MOD;
}类似的题目也都是类似的思路。
无向图中的双联通分量
此部分内容为个人理解。
请注意 辨别 其中的正确性。
如果您认为是错误的那应该就是错误的。若您有心情可以在评论区指出。
无向图中只要有边的那一定是联通分量。双联通分量定义依靠点/边的区分。(下面详细)
其中的共性的是:
- 相对于有向图将会取消交叉边。因为会是其他的边。
边双联通分量(E-DCC)
性质
- 对于一个 E-DCC 我们删除任意边保证剩下 E-DCC 中的任意两点可以互达并且至少在删除任意一条边后。
- 缩点后是一棵树
例题
P8867 建造军营
我们考虑通过 E-DCC 然后进行缩点。
我们考虑树形dp, 不妨定义 $f_{u, i}$ 表示在以点 $i$ 为根的子树 , 是否建造军营 $(j = 0/1)$ 的方案数。
我们先考虑 $f_{u, 0}$ (没有子树被选中)那么对于该子树的方案数任意选择所有边决定是否驻扎军营即为 $\prod f_{ver, 0} * 2$
我们再考虑 $f_{u, 1}$ (有子树被选中)那么我们考虑子树可以选或者不选。那么我们还需要再次思考自然得到 $\prod 2 * f_{ver, 0} + f_{ver, 1}$
我们考虑丢掉了什么情况:就是 $u$ 不选但其他点有可能选的方案数。所以我们考虑前面的所有 $f_{u, 0} * f_{ver, 1}$ 的情况。即为前面的都不选,看当前点。后面的就是后面考虑的事情。那么我们就能解决这道题。
另外就是需要注意本题的初始化。
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
using namespace std;
typedef unsigned long long ll;
const int N = 5e5 + 5, M = 2e6 + 5;
const ll MOD = 1e9 + 7;
int a[N];
int n, m;
int h[M], e[M], ne[M], idx;
int dfn[N], low[N], ts;
int stk[N], top;
int dcc_cnt, dcc[N], dct[N], bs[N];
vector<int> tr[N];
void add(int x, int y) {
e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}
void tarjan(int u, int pid) {
dfn[u] = low[u] = ++ ts;
stk[ ++ top] = u;
for (int i = h[u]; ~i; i = ne[i]) {
int ver = e[i], h = i ^ 1;
if (!dfn[ver]) {
tarjan(ver, h);
low[u] = min(low[u], low[ver]);
} else if (i != pid) {
low[u] = min(low[u], dfn[ver]);
}
}
if (dfn[u] == low[u]) {
++ dcc_cnt;
while (true) {
int v = stk[top --];
dcc[v] = dcc_cnt;
dct[dcc_cnt] ++ ;
if (v == u) {
break;
}
}
}
}
ll f[N][2];
int sz[N];
ll res;
ll qpow(ll x, ll y) {
ll res = 1;
if (y < 0) {
return 0;
}
while (y) {
if (y & 1) {
res = res * x % MOD;
}
x = x * x % MOD;
y >>= 1;
}
return res;
}
void dfs(int u, int fa) {
for (int ver : tr[u]) {
if (ver == fa) {
continue;
}
dfs(ver, u);
(f[u][1] *= (2 * f[ver][0] % MOD + f[ver][1] % MOD)) %= MOD;
(f[u][1] += f[u][0] % MOD * f[ver][1] % MOD) %= MOD;
(f[u][0] *= (2 * f[ver][0] % MOD)) %= MOD;
}
if (u == 1) {
(res += f[u][1] % MOD) %= MOD;
} else {
(res += f[u][1] % MOD * qpow(2, sz[1] - sz[u] - 1) % MOD) %= MOD;
}
}
void dfa(int u, int fa) {
sz[u] = bs[u];
for (int ver : tr[u]) {
if (ver == fa) {
continue;
}
dfa(ver, u);
sz[u] += sz[ver] + 1;
}
}
int main() {
//
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 1; i <= m; i ++ ) {
int u, v;
cin >> u >> v;
add(u, v);
add(v, u);
}
tarjan(1, -1);
int ct = 0;
for (int i = 1; i <= n; i ++ ) {
for (int j = h[i]; ~j; j = ne[j]) {
int ver = e[j];
if (dcc[i] != dcc[ver]) {
tr[dcc[i]].push_back(dcc[ver]);
} else {
bs[dcc[i]] ++;
}
}
}
for (int i = 1; i <= dcc_cnt; i ++ ) {
bs[i] /= 2;
f[i][0] = qpow(2, bs[i]) % MOD;
f[i][1] = (qpow(2, bs[i] + dct[i]) % MOD + MOD - f[i][0]) % MOD;
}
dfa(1, -1);
dfs(1, -1);
cout << res % MOD;
return 0;
}点双联通分量(V-DCC)
定义
- 对于无向图上去掉一个点。使得剩下图中联通分量增加了。这个点就是点双联通分量。
应用
- VDCC比较常用的是圆方树。我们考虑建的方法是把所有点和点联通分量相连。最终会构成一棵树。貌似是往次WC提出来的算法。
圆方树的性质
树上任意两点的路径是必经路径。也就是任意路线必然会经过这些点。可以在题目简化后对这些点进行处理。
有了这个性质大部分题目也就可以解决。
Done.
1 条评论
前排