首先呢,这道题我们肯定不能暴力枚举。枚举a、b左右端点,这样做的时间复杂度很高,大约为$O(n^3)$显然超时.
$$ test $$
超时代码比想象中的分高, 洛谷得分$\color{orange}{60}$。
//
// Created By smallfang.
//
#include <iostream>
#include <cstdio>
using namespace std;
const int MAXN = 200000;
int pr[MAXN + 5], cl[MAXN + 5], res = 0;
int main()
{
int n, k, p;
scanf("%d%d%d", &n, &k, &p);
for (int i = 1; i <= n; i ++ )
{
scanf("%d%d", &cl[i], &pr[i]);
}
int res = 0;
for (int i = 1; i <= n; i ++ )
{
for (int j = i + 1; j <= n; j ++ )
{
if (cl[i] != cl[j])
{
continue;
}
bool flag = false;
for (int fk = i; fk <= j; fk ++ )
{
if (pr[fk] <= p)
{
flag = true;
break;
}
}
if (flag == true)
{
res ++;
}
}
}
printf("%d", res);
return 0;
}显然我们我们为了100分,需要更加优化的做法。我们先从配对的基本要求入手。
基本要求:
- $a$与$b$的颜色完全相等。
- 这个之间有符合要求的酒馆,价格要小于规定的$k$
首先咱们来看第2个要求。这个之间有符合要求的酒馆。那么我们是不是可以倒推出来。只要有一个酒馆符合条件,那么,包含这个酒馆的两个$a$, $b$就一定能满足条件2。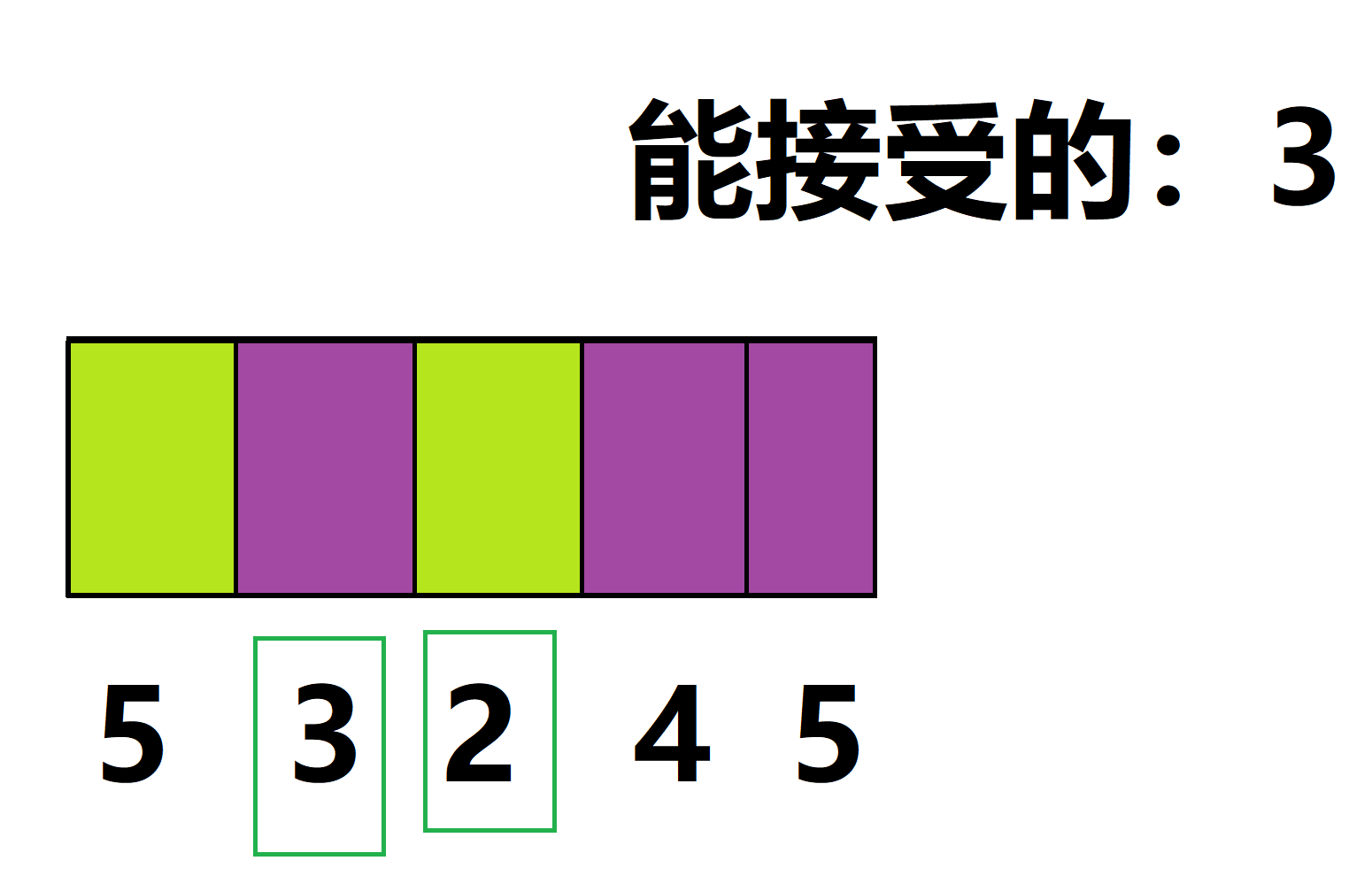
显然,被框住的数字是可以接受的。我们需要记录从这些被框住的数字开始,倒退往前。在这个过程中,所有出现过的颜色,颜色个数+1(代表该颜色已经满足了题目要求2的条件的个数)。原因是:每次都是往后找,不会出现往前找的情况,所以,每次加上该颜色在之前中,符合了题目要求2的个数即$res[color]$。
其次,我们需要考虑”到底走到哪里为结束“。
我们通过分析,不难得到,只需要走到上次被框住的位置。因为上次框住的位置到它之前,以前被这个上个框住的位置标记过了,不能重复标记。
另外,走到上一个被标注的位置,是不对的。因为题目要求两点直接也算数。所有在更新时应该是到上一个被标注的位置的上一个。
最后,由于题目要求,每次走到的点,上的$color[i]$需要减1,因为,两个人不能站在一起。
第一个被标注的位置,的上一个被框住的位置是0。
如果你被上面的那句话绕晕了,那就看看下面的图: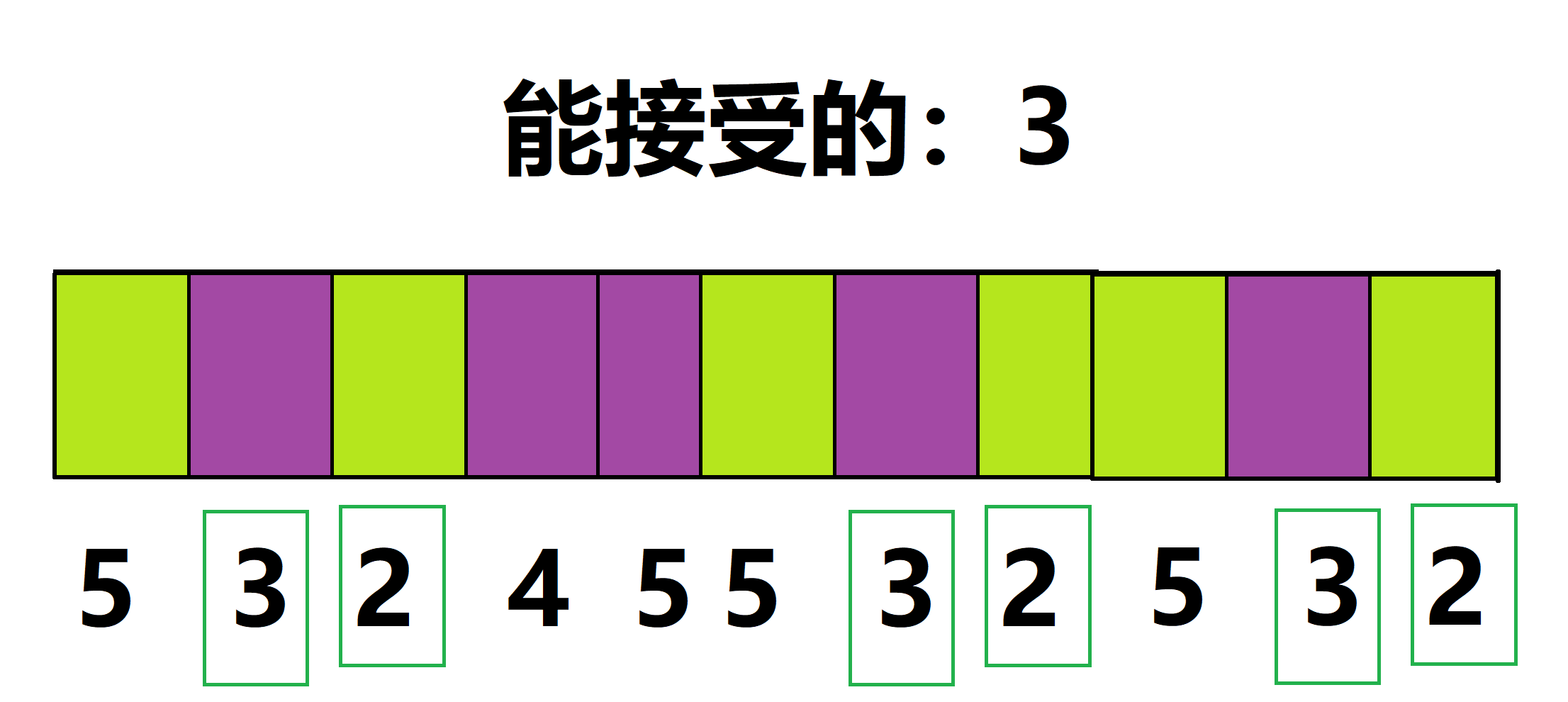
首先我们从输入中得到5。
发现这个数不符合要求二。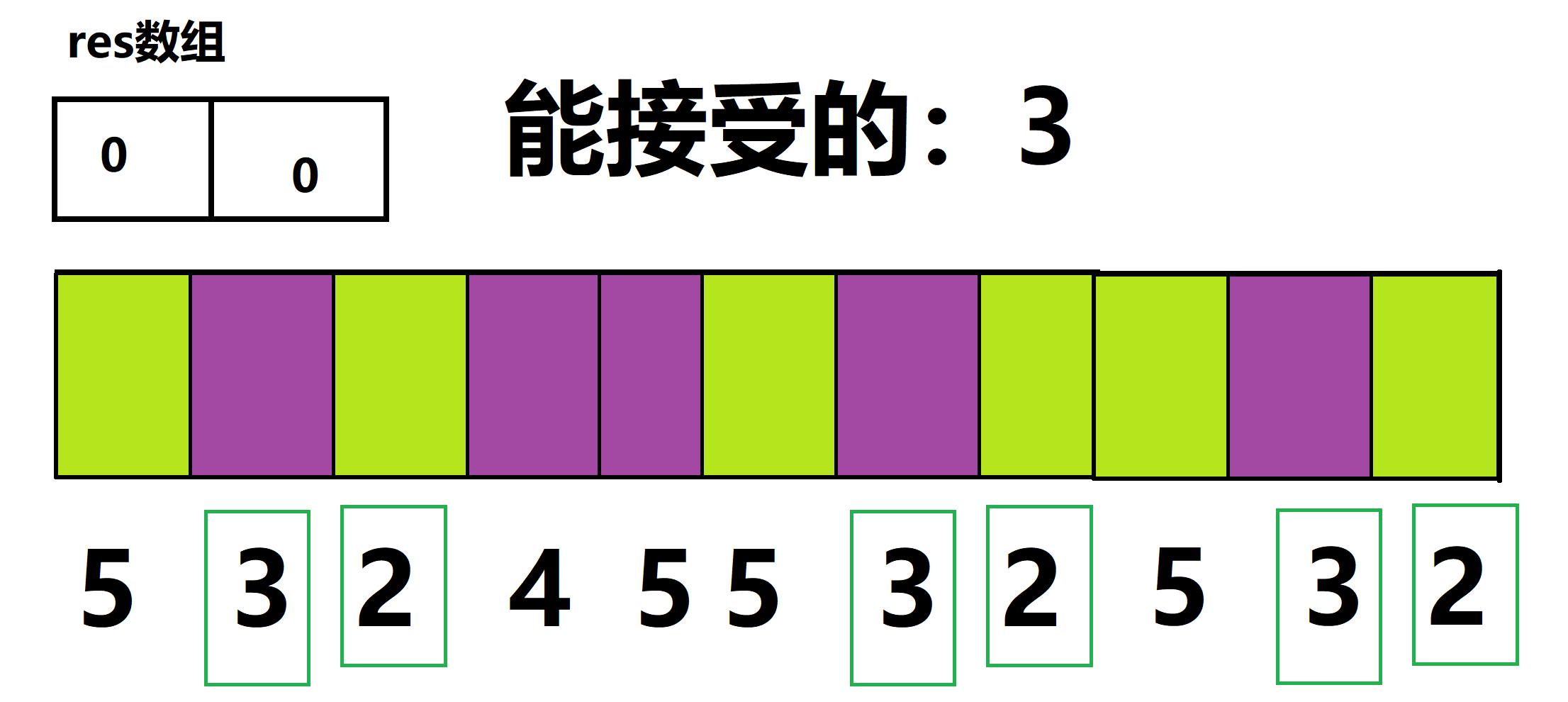
那么我们继续读入3,发现它符合要求。那么我们从它开始,向前寻找。找到上一个位置0。$ans = ans + 1 - 1 = 0$
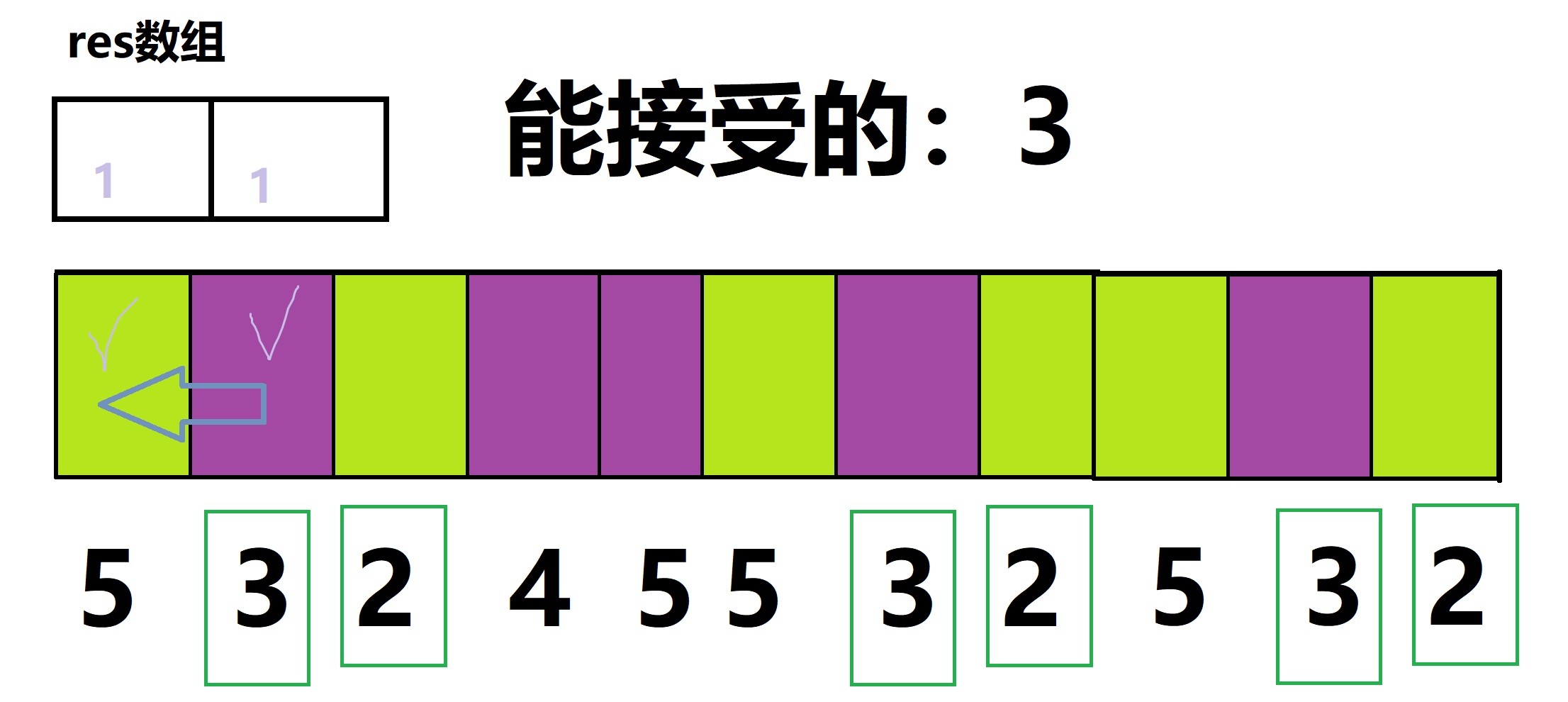
那么我们继续读入2,发现它符合要求。那么我们从它开始,向前寻找。找到上一个位置2。$ans = ans + 2 - 1 =1$
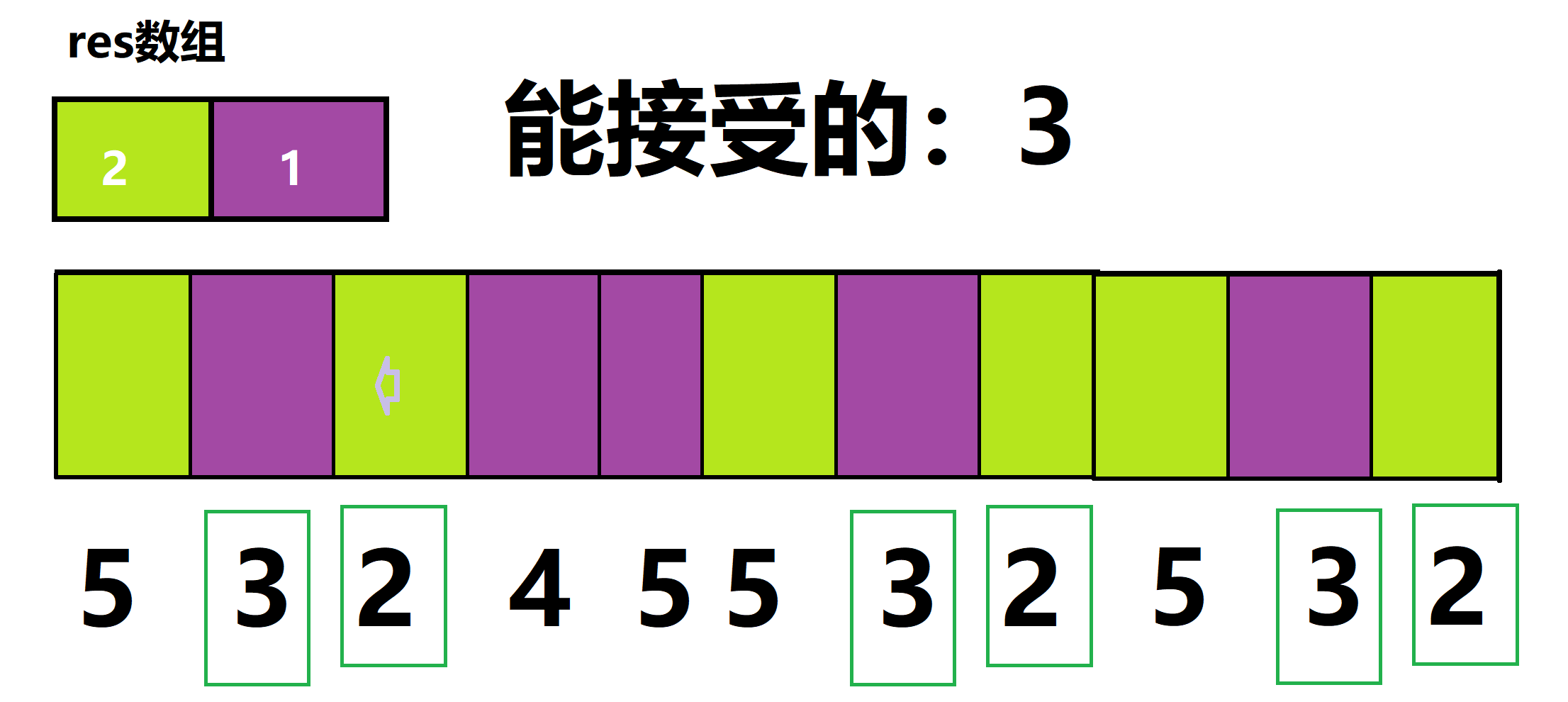
读入4,$ans = ans + 1 = 2$
读入5,$ans = ans + 1 = 3$
读入5,$ans = ans + 2 = 5$
那么我们继续读入3,发现它符合要求。那么我们从它开始,向前寻找。找到上一个位置3。.
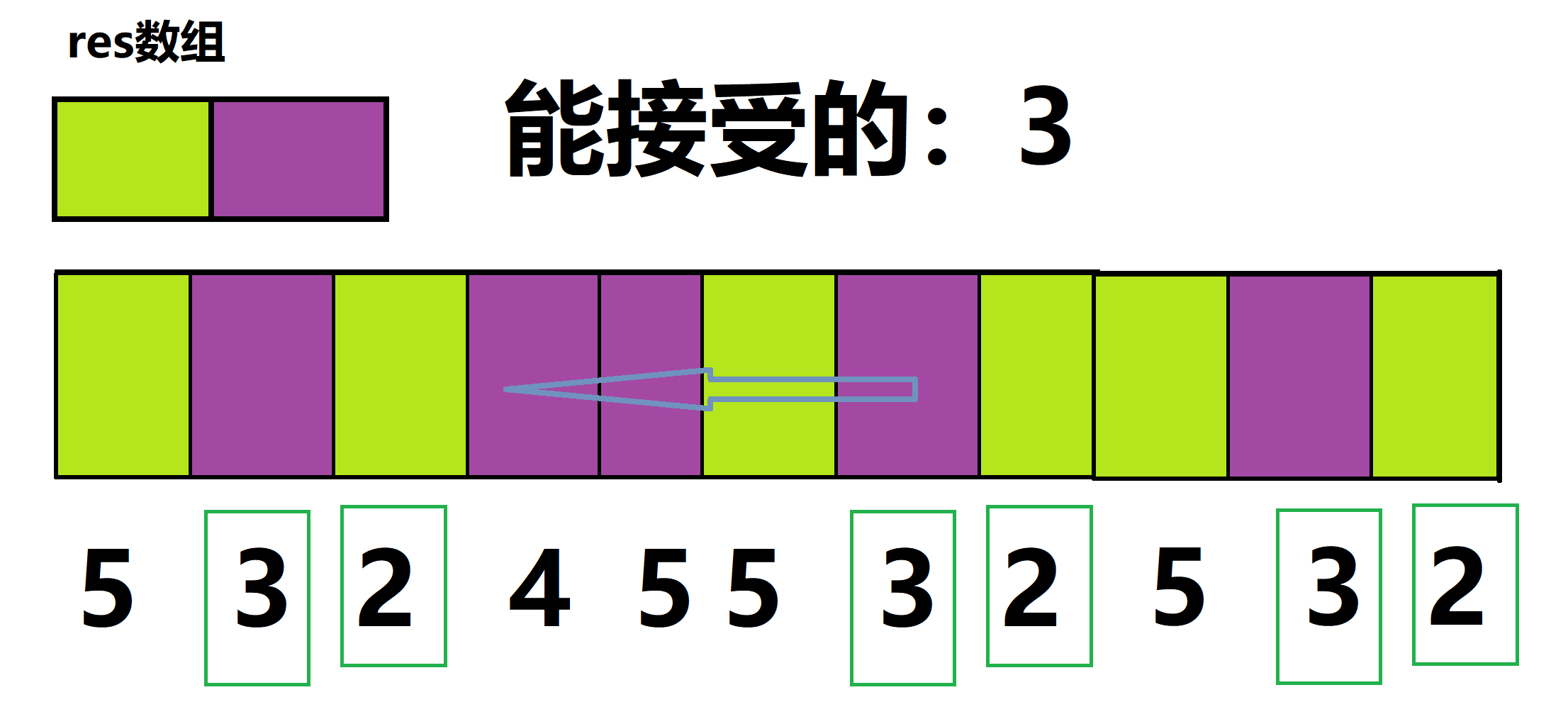
//
// Created By smallfang.
//
#include <iostream>
#include <cstdio>
using namespace std;
const int MAXN = 200000;
int res[MAXN + 5], cl[MAXN + 5], ans = 0;
int main()
{
int n, k, p;
scanf("%d%d%d", &n, &k, &p);
int w = 0;
for (int i = 1; i <= n; i ++ )
{
int b;
scanf("%d%d", &cl[i], &b);
if (b <= p)
{
for (int j = i; j > w; j -- )
{
res[cl[j]] ++;
}
w = i;
}
ans += res[cl[i]] - (b <= p);
}
printf("%d", ans);
return 0;
}至此,这道题就做完了(
应该质量挺高的吧((((