P5459

问题转换：

=> 求多少个符合规则($R≥子区间的和≥L$)子区间。

思路：

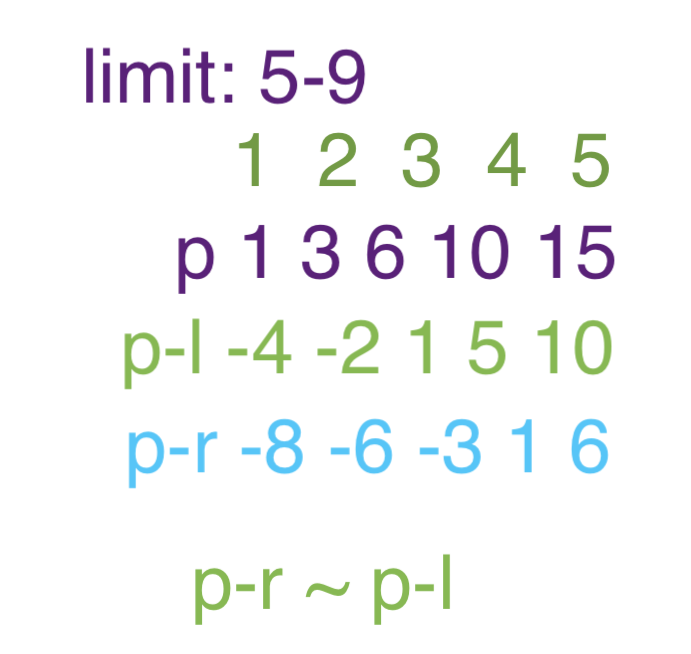
请您将所有的p想象成q.

我们在统计前缀和时，有$q_i=q_1+q_2+...+q_i$

当我们想知道都多少答案符合要求时，我们不妨按$q$的顺序来找找看。

遍历每次$q_i$，寻找以$q_i$为结尾的答案有多少个。

那么我们需要在$q_i$前找到一个$q_j$使得$q_i-q_j$符合答案的≥$L$,≤$R$.

那么什么情况下这个$q_j$符合要求呢...

我们可以简单的化简一下式子。

$R≥q_i-q_j≥L$

$q_i≥L+q_j$

$q_i-L≥q_j$

$q_i-R≤q_j$

所以我们伟大的得到了

$q_i-L≥q_j≥q_i-R$

也就是说只要有在$q_i-R$与$q_i-L$范围内，该值一定符合要求。

我们可以排序然后离散化，这样就可以依次的查找所有的前缀和，然后是从小到大每次依次插入到树状数组即可。（该过程说的有点抽象可以看实现）

实现具体过程：

现将$0$插入$a$数组。

依次将将$q_i, q_i-l, q_i - r$插入到数组$a$(最后需要离散化)。($q$数组指前缀和)

将$a$数组离散化

将数组中0的位置增加1.

从$1-n$遍历寻找$q_i,q_i-r,q_i-l$的位置。

每次将答案加上$q_i-r到q_i-l$的和。

当然如果想的话是可以拿线段树过的（（

当然据说这题是个cdq水题。

code

// Problem: P5459 [BJOI2016]回转寿司
// URL: https://www.luogu.com.cn/problem/P5459
// Memory Limit: 250 MB
// Time Limit: 1000 ms
// smallfang.

#include <cctype>
#include <iostream>
#include <climits>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 6e5 + 5;

long long a[N], c[N], m, q[N], x;

int lowbit(int x)
{
    return x & (-x);
}

int query(int x, int y)
{
    int res = 0;
    while (y)
    {
        res += c[y];
        y -= lowbit(y);
    }
    x --;
    while (x)
    {
        res -= c[x];
        x -= lowbit(x);
    }
    return res;
}

void add(int x, int y)
{
    while (x <= m)
    {
        c[x] += y;
        x += lowbit(x);
    }    
    return ;
}

int main()
{
    int n, l, r;
    cin >> n >> l >> r;
    a[++ m] = 0;
    for (int i = 1; i <= n; i ++ )
    {
        int x;
        cin >> x;
        q[i] = x + q[i - 1];
        a[++ m] = q[i];
        a[++ m] = q[i] - l;
        a[++ m] = q[i] - r;
    }
    sort(a + 1, a + 1 + m);
    m = unique(a + 1, a + 1 + m) - (a + 1);
    long long res = 0;
    add(lower_bound(a + 1, a + 1 + m, 0) - a, 1);
    for (int i = 1; i <= n; i ++ )
    {
        int x = lower_bound(a + 1, a + 1 + m, q[i] - r) - a;
        int y = lower_bound(a + 1, a + 1 + m, q[i] - l) - a;
        int z = lower_bound(a + 1, a + 1 + m, q[i]) - a;
        res += query(x, y);
        add(z, 1);
    }
    cout << res;
    return 0;
}