【咕咕咕】

概念

流网络

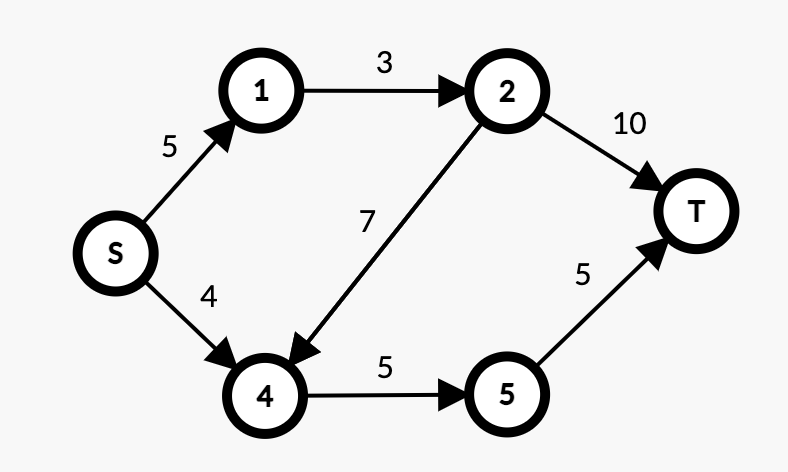
倒是费了半天劲画了个图

这个有向图就是一个流网络。并且我们在接下来的讨论中默认没有自环（默认没有反向边）(即u->v后无v->u的边)。主要是可能比较更加的难理解。我们记录该流网络 $G=(V,E)$即所有的点集$V$和边集$E$。

容量

参考上图，其中每两个点之间上的值就叫流量。例如，上图中点S->点1的容量为5.记作 $c(s,1)=5$

一般的记录为$c(u,v)$。

流量

同样参考上图，但是这个流量是可以定义的。例如我们可以假设点S->点1的流量为5。记作$f(s,1)=5$一般的记录为$s(u,v)$

可行流

当我们知道了前面的定义，我们可以开始定义可行流。当这个流网络符合以下规则即为可行流。同样不考虑反向边

1. $f(u,v)≤c(u,v)$ 即所有边的流量都应该小于对应边的容量。（容量限制）
2. $ \sum_{E \in (u,v) \notin S,T}f(u,v)=\sum_{E \in (v,x) \notin S,}f(v,x)$ [heimu]可能不太会写公式[/heimu]大概就是所有入的变的流量等于出边的流量（流量守恒）

符合以上规则的流网络即为可行流

最大可行流

顾名思义就是求$max\{sum_{f(s,v)}\}$（最大的所有从起点出的流量）

残留网络

此处会应用到反向边。

此处反向边的作用是（给网络流一个反悔的可能）

那么残留网络是怎么操作的呢：

1. 保留点集$V$，删除边集$E$
2. 将所有原有边集有向边$(u,v)$连权为$f(u,v)$（流量），$from=u,to=v$即$u-^{E(u,v)}->v $。
3. 将所有原有边集有向边$(u,v)$连反向边为$c(u,v)-f(u,v)$,$from=u,to=v$即 $v -^{\space 0}->u$

记残留网络为$G_f$，其中$f$是原有可行流。

关于残留网络相关的定理

残留网络本身就是一种可行流。所以记残留网络为$f'$.

增广路

沿着非零的可行流$f(u,v)$走，能从$S$（起点）走到$T$（终点）。

性质：最大可行流没有增广路

割

将整个图的点集保留，将所有边分为2部分。容量指代一部分流出到另一部分的流量。
最小割指代求这个值容量最小。

做法

最大流最小割定理

由于我已经不会证了

但是其中最重要的一点是：残留网络没有增广路是最大流必要充分条件。

所以引出了我们亲爱的FF方法

就是直接初始化残留网络。然后增广。使其不能再增广。

此时我们引出如何求最大流（=最大可行流）。

EK求最大流

EK算法即为初始化残留网络。每次寻找增广路。增广这条边。

直到无法再增广，此时即为答案。

理论时间复杂度 $O(n^{2}m)$ 但其实根本跑不满，基本可以处理 $1000$ 级别的网络

dinic 求最大流

Dinic 是EK算法的优化。每次找所有能增广的路。

理论时间复杂度 $O(nm^{2})$，基本可以处理 $10000$ 左右的网络

ISAP / 递流推进

// TODO: 需要学习。

大概率现在网络流基本上不卡Dinic。所以基本上不会用到ISAP 递流推进。