最小生成树
过20天没更博客了...感觉还没几天呢....
概述:
在一张图中找到一棵路径和最短的树。
算法实现:
Prim与Kruskal算法。
在这里我们主要讲解一下Prim算法。
Prim算法实现概述
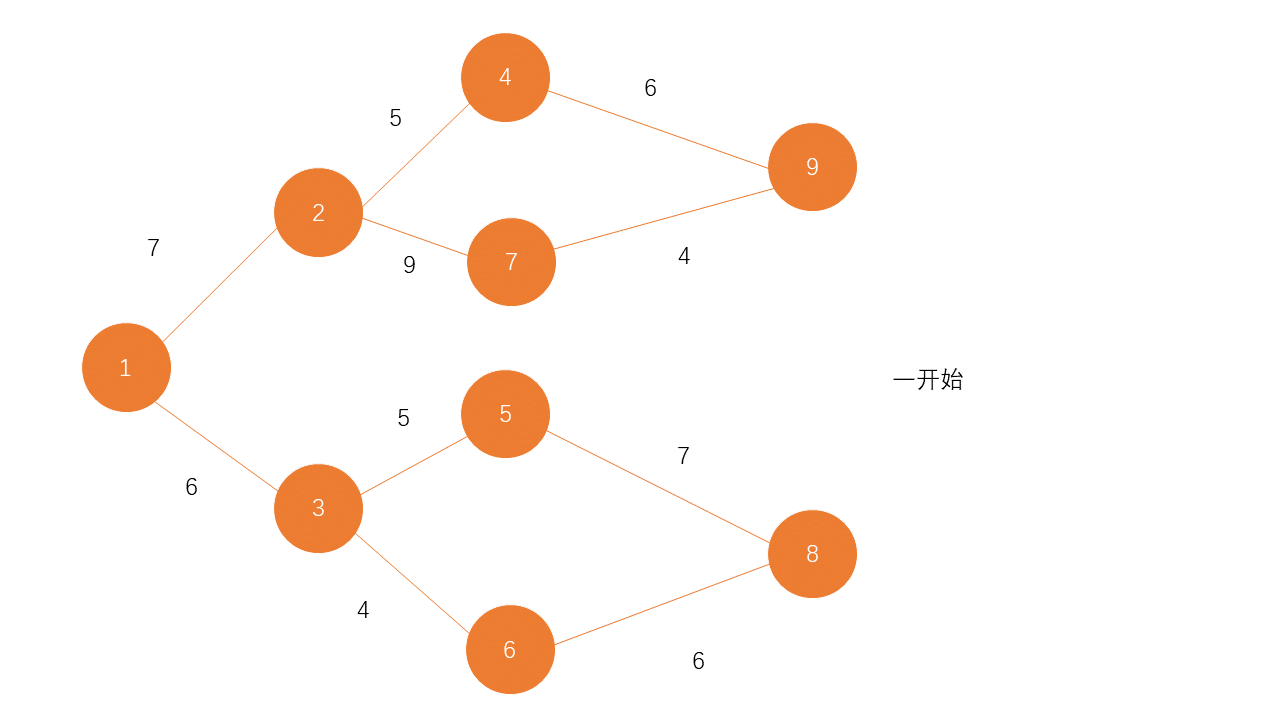
一个贪心类的方法。每次选择一个点开始。寻找能找到的最小的点。
Prim 算法实现模拟
 (https://cdn.rotriw.cn/smallfang/uploads/2020/05/2686506118.png)(https://blog.smallfang.fun/usr/uploads/2020/05/2686506118.png)
(https://cdn.rotriw.cn/smallfang/uploads/2020/05/2686506118.png)(https://blog.smallfang.fun/usr/uploads/2020/05/2686506118.png)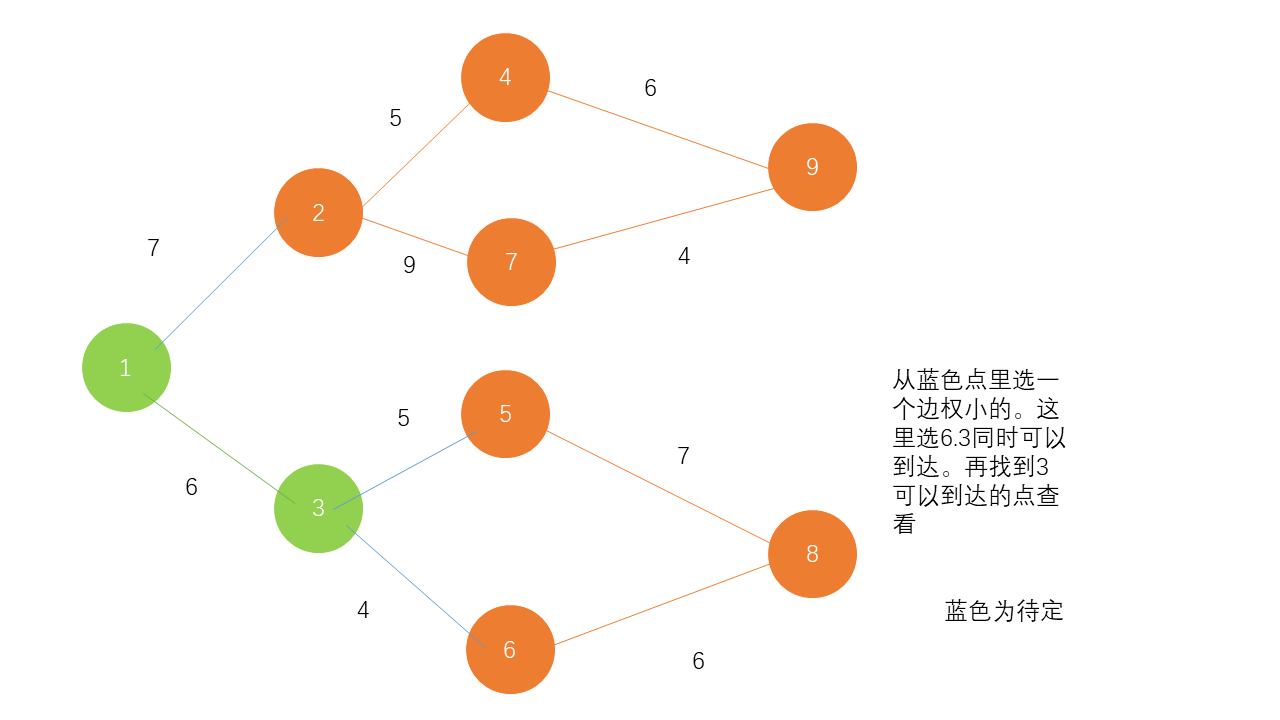 (https://cdn.rotriw.cn/smallfang/uploads/2020/05/943343188.png)(https://blog.smallfang.fun/usr/uploads/2020/05/943343188.png)
(https://cdn.rotriw.cn/smallfang/uploads/2020/05/943343188.png)(https://blog.smallfang.fun/usr/uploads/2020/05/943343188.png) (https://cdn.rotriw.cn/smallfang/uploads/2020/05/943343188.png)(https://cdn.rotriw.cn/smallfang/uploads/2020/05/943343188.png)
(https://cdn.rotriw.cn/smallfang/uploads/2020/05/943343188.png)(https://cdn.rotriw.cn/smallfang/uploads/2020/05/943343188.png)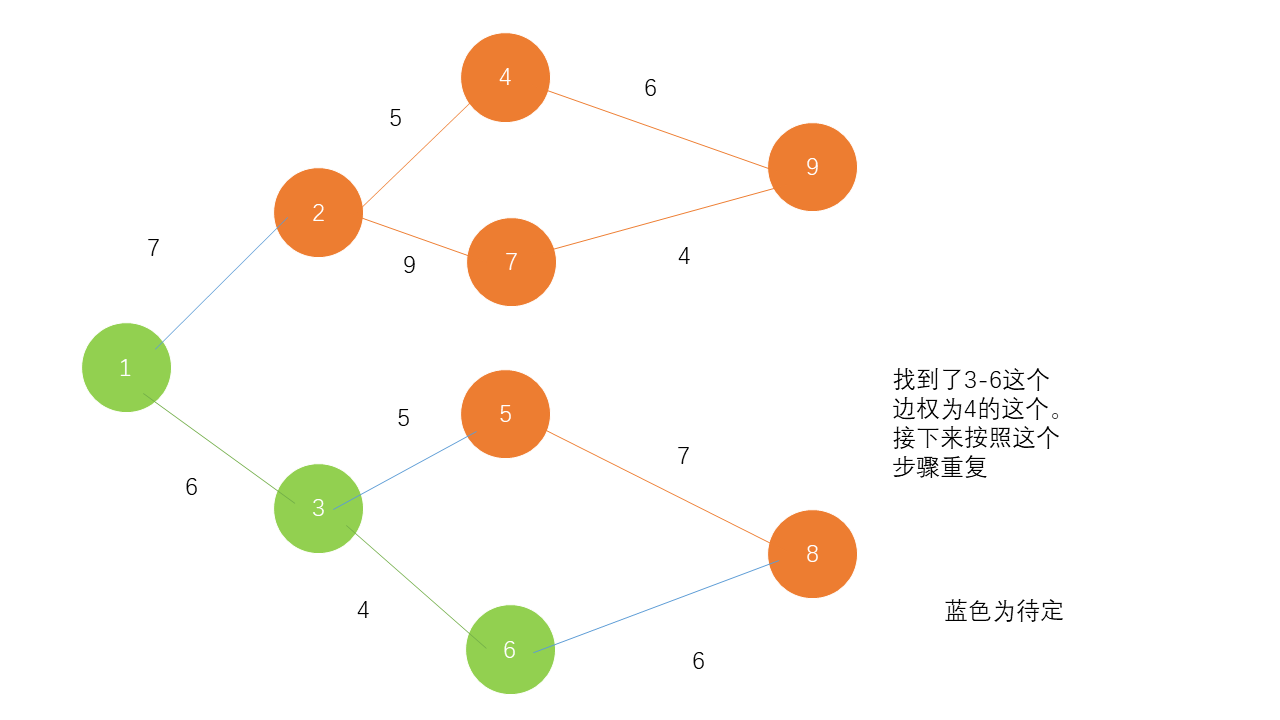 (https://cdn.rotriw.cn/smallfang/uploads/2020/05/3653047268.png)(https://blog.smallfang.fun/usr/uploads/2020/05/3653047268.png)
(https://cdn.rotriw.cn/smallfang/uploads/2020/05/3653047268.png)(https://blog.smallfang.fun/usr/uploads/2020/05/3653047268.png) (https://cdn.rotriw.cn/smallfang/uploads/2020/05/2778039670.png)(https://cdn.rotriw.cn/smallfang/uploads/2020/05/2778039670.png)
(https://cdn.rotriw.cn/smallfang/uploads/2020/05/2778039670.png)(https://cdn.rotriw.cn/smallfang/uploads/2020/05/2778039670.png)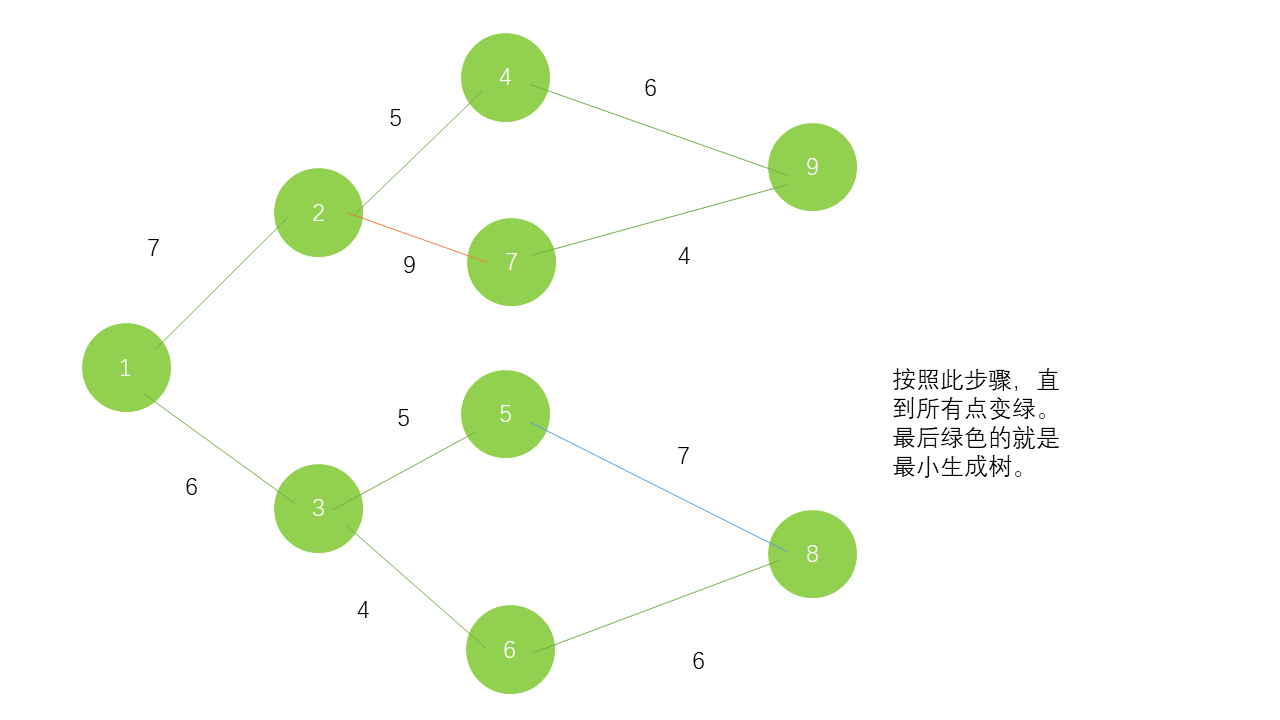 (https://cdn.rotriw.cn/smallfang/uploads/2020/05/1962599864.png)(https://cdn.rotriw.cn/smallfang/uploads/2020/05/1962599864.png)
(https://cdn.rotriw.cn/smallfang/uploads/2020/05/1962599864.png)(https://cdn.rotriw.cn/smallfang/uploads/2020/05/1962599864.png)
算法实现
通过图片可知的算法。Code:
#include <iostream>
#include <cstring>
#include <stack>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
int n, m, k;
bool use[31];
vector<pair<int,int> > g[31];
struct node
{
int x, y;
int l;
bool operator < (const node &b) const
{
return l > b.l;
}
};
int prim()
{
int res = 0;
int s = 1;
int con = 1;
use[s] = true;
int t = s;
priority_queue<node> q;
for(int i = 1; i < n; i ++ )
{
for(int i = 0; i < g[t].size(); i ++ )
{
if(use[g[t][i].first] == false)
{
node ne;
ne.l = g[t][i].second;
ne.x = t;
ne.y = g[t][i].first;
q.push(ne);
}
}
node e;
do
{
e = q.top();
q.pop();
} while (use[e.y] == true);
res += e.l;
use[e.y] = true;
t = e.y;
}
return res;
}
int main()
{
queue<int> q;
q.push(1);
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; i ++ )
{
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
g[x].push_back(make_pair(y, z));
g[y].push_back(make_pair(x, z));
}
printf("%d", prim());
return 0;
}